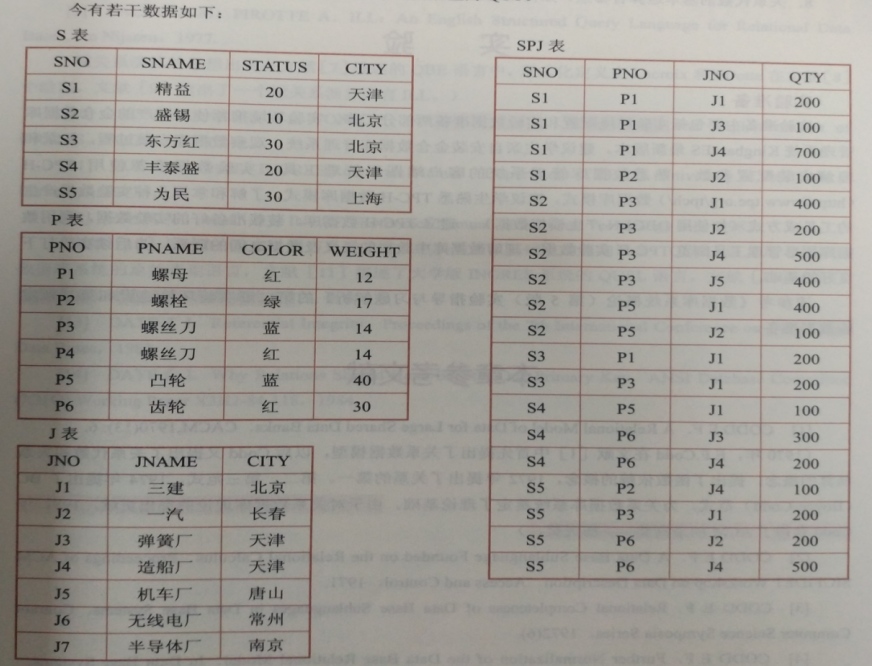
数据
数据库
1
| 长期存储在计算机内、有组织的、可共享的大量数据的集合
|
DBMS(Database Manager System)
1
| 数据库管理软件。如mysql,sqlserver,mariadb,Access等等内部都内置了各种的DBMS,所以也称这些都是DBMS,换言之,目前流行的DBMS有mysql,sqlserver等等
|
DBS
1
| 数据库系统也简称为数据库。由数据库,DBMS及其开发工具、应用程序(如学生管理系统的前台界面)、DBA及其用户构成
|
数据模型
1
2
| (1)概念模型:按照用户的观点来对数据和信息建模(很重要,会影响到逻辑模型和物理模型)
(2)逻辑模型和物理模型:主要包括网状模型、层次模型、关系模型等,它是按照计算机系统的观点对数据建模。用于DBMS的实现
|
数据模型的组成要素
1
2
3
| 1.数据结构
2.数据操作
3.数据的约束条件
|
实体
属性
码
域
实体型
1
| 实体名及其属性名集合来抽象刻画同类实体。如学生(姓名 学号 班级)就是一个实体型
|
实体集
概念模型标识方法
数据库系统的三级模式
1
| 模式(逻辑模式)是全体数据,外模式(子模式)是全体数据中的某一部分,内模式也称存储模式
|
外模式/模式映像
1
2
3
| 定义了外模式与模式之间的对应关系
每个外模式都对应一个外模式/模式映像(映像数量多个)
映像定义通常包含在各自外模式的描述中
|
模式/内模式映像
1
2
3
| 定义了数据全局逻辑结构与存储结构之间的对应关系
数据库中模式/内模式映像是唯一的
该映像的定义通常包含在模式描述中
|
关系数据模型
其数据结构是一张二维的表格
候选码
主属性
定义:包含在任何候选码中的属性(主码一定是候选码,候选码不一定是主码,因为主码是人选的,是随机的)
例:比如,竞赛表(竞赛编号,竞赛名称,竞赛组织者) PS:竞赛名称和竞赛组织者都可以重复
很明显可以看出竞赛编号能够唯一标识整张竞赛表,因此候选码是竞赛编号,并且仅此一个候选码,其他属性都不能唯一标识整张表,所竞赛编号同时也是主码。
这时候判断一下这几个属性 or 属性组是否是主属性,(竞赛编号)(竞赛编号,竞赛名称)(竞赛名称,竞赛组织者),(竞赛编号)只有一个属性,这个属性是主码,主码必定为候选码,因此属性含有一个候选码,这个属性是主属性。(竞赛编号,竞赛名称)有两个属性,其中竞赛编号是候选码,而竞赛名称不是候选码,那他是啥呢~前面有提到了,因为它跟候选码在同一个属性组里,所以,竞赛名称是超码,回过头来,最后得出该属性组含有了一个候选码,因此该属性组中的各个属性都是主属性。(竞赛名称,竞赛组织者)有两个属性,可以看出这两个属性都不是候选码,因此这个属性组不包含候选码,属性组中中得各个元素称为非主属性。
misc
1
| 主码=主键=主关键字,关键字=候选码 候选关键字=候选码中除去主码的其他候选码
|
分量
1
| 如在二位表格中的单元格的值。关系的分量必须是一个不可分的数据项(如工资被分为奖金、工龄、基本,这样对于关系来说是不规范的)
|
元组
1
| 表中的每行(即数据库中的每条记录)就是一个元组;元组的个数为基数
|
目(度)
关系模型中的三类完整性约束
1
2
3
| 1. 实体完整性
2. 参照完整性
3. 用户定义完整性
|
实体完整性
1
| 实体完整性规则规定基本关系的所有主属性不能取空值,当我给某个表设置主键时,由于给主属性设置了空值,始终创建不了主码
|
参照完整性
1
| 在关系模型中实体与实体之间的联系都是用关系来描述的,因此存在关系与关系之间的引用
|



外码
设F是基本关系R中的一个或一组属性,但不是关系R的码。如果F与基本关系S中的主码K相对应,那么F是基本关系R的外码(外码取值可取空值,因为不是主属性;外码可取S中某个元组的主码值)
参照关系
外码所在的关系,即关系R为参照关系
被参照关系(目标关系)
关系S为参照关系
例 1
外码:专业 参照关系:学生关系 被参照关系:专业关系
例 2
外码:学号、课程号 参照关系:选修 被参照关系:学生关系、课程关系
例 3
外码:班长 参照关系:学生关系 被参照关系:学生关系
用户定义完整性
1
2
3
4
| 例:课程(课程号,课程名,学分) 主码为课程号
- “课程名”属性必须取唯一值
- 非主属性“课程名”不能取空值
- “学分”属性只能取值{1,2,3,4}
|
关系代数运算的分类
1
2
| 1.传统的集合运算:并、交、差、广义笛卡尔积
2.专门的关系运算:选择、投影、连接、除
|
运算符及其对应关系
| 运算符 | 含义 |
|---|
| ∪ | 并 |
| - | 差 |
| ∩ | 交 |
| × | 笛卡尔积 |
| σ | 选择 |
| π | 投影 |
| ⋈ | 连接 |
| ÷ | 除 |
专门的关系运算
记号
R, t∈ R, t[Ai]
- 设关系模式为 R(A1,A2,……,An)
- t∈ R 表示 t 是 R 的一个元组
- t[Ai]表示元组 t 中对应属性 Ai的一个分量(单元格的值)
A, t[A], $\overline{A}$
若 A={Ai1,Ai2,……,Aik}
- 其中 A 称为属性列或者域列
- t[A]=([t[Ai1],t[Ai2],……,t[Aik])表示元组 t 在属性列 A 上诸分量的集合
- $\overline{A}$表示{A1,A2,……,An}中去掉{Ai1,Ai2,……,Aik}后剩余的属性列

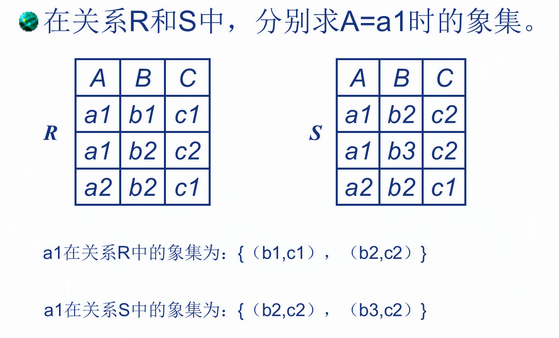
象集
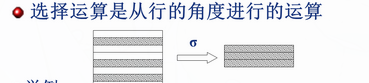
选择
| Sno | Sname | Ssex | Sage | Sdept |
|---|
| 201215122 | 刘晨 | 女 | 19 | IS |
| 201215125 | 张立 | 男 | 19 | IS |
| 201215122 | 王敏 | 女 | 19 | MA |
| 201215122 | 李勇 | 男 | 19 | CS |
| 201215122 | 大地 | 男 | 20 | IS |
例 1 查询信息系(IS)全体学生的信息
$$\sigma_{Sdept=‘IS’}(Student)$$ (字符串使用单引号)
| Sno | Sname | Ssex | Sage | Sdept |
|---|
| 201215122 | 刘晨 | 女 | 19 | IS |
| 201215125 | 张立 | 男 | 19 | IS |
| 201215122 | 大地 | 男 | 20 | IS |
例 2 查询信息系年龄小于 20的学生信息
$$\sigma_{Sdept=‘IS’\wedge Sage<20}(Student)$$
| Sno | Sname | Ssex | Sage | Sdept |
|---|
| 201215122 | 刘晨 | 女 | 19 | IS |
| 201215125 | 张立 | 男 | 19 | IS |
投影
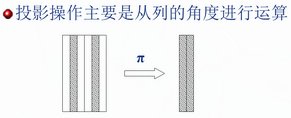
投影后不仅取消了原关系中的某些列,而且还可能取消某些元组(避免重复行)
例 3 求 Student 关系学生姓名和所在系两个属性上的投影:
$$\pi_{Sname,Sdept}(Student)$$
| Sname | Sdept |
|---|
| 刘晨 | IS |
| 张立 | IS |
| 王敏 | MA |
| 李勇 | CS |
| 大地 | IS |
例 4 查询学生关系 Student 中都有哪些系?(涉及去重)
$$\pi_{Sdept}(Student)$$
思考:查询信息系年龄<20 岁的学生学号、姓名、年龄?
$$\pi_{Sno,Sname,Sage}(\sigma_{Sdept=‘IS’\wedge Sage<20}(Student))$$
连接(join)
1.普通连接
关系 R
关系 S

两关系做笛卡尔积后结果为
| A | R.B | C | S.B | E |
|---|
| a1 | b1 | 5 | b1 | 3 |
| a1 | b1 | 5 | b2 | 7 |
| a1 | b1 | 5 | b3 | 10 |
| a1 | b1 | 5 | b3 | 2 |
| a1 | b1 | 5 | b5 | 2 |
| a1 | b2 | 6 | b1 | 3 |
| a1 | b2 | 6 | b2 | 7 |
| a1 | b2 | 6 | b3 | 10 |
| a1 | b2 | 6 | b3 | 2 |
| a1 | b2 | 6 | b2 | 2 |
| a2 | b3 | 8 | b1 | 3 |
| a2 | b3 | 8 | b2 | 7 |
| a2 | b3 | 8 | b3 | 10 |
| a2 | b3 | 8 | b3 | 2 |
| a2 | b3 | 8 | b5 | 2 |
| a2 | b4 | 12 | b1 | 3 |
| a2 | b2 | 12 | b2 | 7 |
| a2 | b2 | 12 | b3 | 10 |
| a2 | b2 | 12 | b3 | 2 |
| a2 | b2 | 12 | b5 | 2 |
根据C<E,筛选后得
| A | R.B | C | S.B | E |
|---|
| a1 | b1 | 5 | b2 | 7 |
| a1 | b1 | 5 | b3 | 10 |
| a1 | b2 | 6 | b2 | 7 |
| a1 | b2 | 6 | b3 | 10 |
| a2 | b3 | 8 | b3 | 10 |
2.等值连接

| A | R.B | C | S.B | E |
|---|
| a1 | b1 | 5 | b1 | 3 |
| a1 | b2 | 6 | b2 | 7 |
| a1 | b2 | 6 | b2 | 2 |
| a2 | b3 | 8 | b3 | 10 |
| a2 | b3 | 8 | b3 | 2 |
| a2 | b2 | 12 | b2 | 7 |
3.自然连接
是一种特殊的等值连接

| A | B | C | E |
|---|
| a1 | b1 | 5 | 3 |
| a1 | b2 | 6 | 7 |
| a1 | b2 | 6 | 2 |
| a2 | b3 | 8 | 10 |
| a2 | b3 | 8 | 2 |
| a2 | b2 | 12 | 7 |
自然连接与等值连接区别:
- 等值连接中不要求相等属性值的属性名相同,而自然连接要求相等属性值的属性名必须相同,即两关系只有在同名属性才能进行自然连接。如上例 R 中的 C 列和 S 中的 E 列可进行等值连接,但因为属性名不同,不能进行自然连接。
- 等值连接不将重复属性去掉,而自然连接去掉重复属性,也可以说,自然连接是去掉重复列的等值连接。如上例 R 中的 B 列和 S 中的 B 列进行等值连接时,结果有两个重复的属性列 B,而进行自然连接时,结果只有一个属性列 B
选择、投影、(自然)连接综合例题

$$\pi_{sno,sname}(\sigma_{cno=‘2’}(student\bowtie sc))$$
除
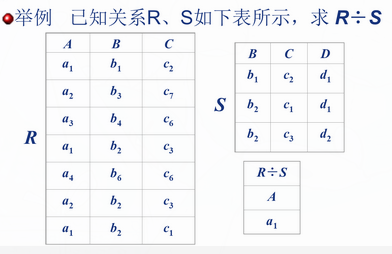

课后习题